Having fussed and struggled my way through the first few levels of Euclidea for blog post 1, I decided on a reset and went back to the beginning. The second time around was not only a bit more “fun” but also more beneficial. The first time through, I was just interested in passing levels. I finally gave up and paid the small fee to open everything (which I’m glad I did… keep reading). This new time around I focused more on the challenge of beating the levels within the “allowable” moves. I was much more comfortable with the process of playing and could focus more on the objectives specifically.
This reflection makes me think the game would benefit from a low-stakes tutorial or sandbox level that allows users to just use the tools, perhaps under guided instruction to make designs that are not actual levels in the game.
After playing and succeeding in the first handful of levels, I decided to peek at the rest of the levels and was pleasantly surprised to find later levels that tied directly to what I had been teaching in class about points of concurrency (incenter and circumcenter). I realized that the game could be incorporated, in bits and pieces, into the curriculum. I would not see it a lesson into itself, but as a challenge or a way to have students practice and recognize some of the features of this concept, in conjunction with the lesson.
Finally, I came across a level called “Napoleon’s Problem”. I’d not heard of this problem before, but after investigating it (thanks Wikipedia), I saw this as a challenge problem that could be used to push students to investigate further into areas that might not be covered in any class. The problem is simply stated – find the center of a circle using only a compass. The simplicity of the problem invites all kinds of efforts to find a solution (efforts that may be frustrating, but are educational even in struggle). Students may try to find the solution on-line, but even in that process, they would be learning and investigating the use of the compass and the logic with which it is employed to solve the problem.
So my opinion remains that this is not the next x-box, but for a class supplement and source of challenge, I could see using it.
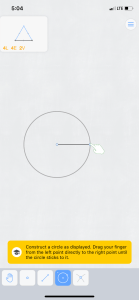
The instructions to help use the tools are pretty sparse. 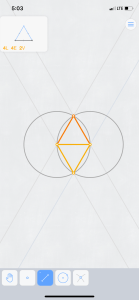
Success! 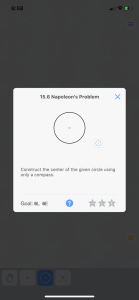
Later levels offer tough challenges. 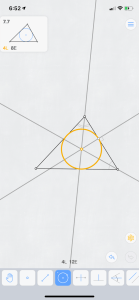
Modeling the incenter. 
Modeling the circumcenter.
This seems like a really cool app/ game that I would have liked to use when I took geometry in high school! You mentioned there was a bit of a learning curve and you had to sort of start over. Do you think students would experience this as well? If so how do you think you would ease this struggle so your students don’t have the frustration process that you had to go through? I was also wondering how you would incorporate differentiation into this as it seems to have a preset of what the challenges are. I am excited to see more updates on this game and if you are considering incorporating it into your own curriculum!
LikeLike
I suppose I picked this game without any particular context in which to use it – other than testing it out. My motivations were thus a bit different than if I were using it as part of a geometry class. I had an experience a couple of semesters ago using a new program in a math class at JCU. I remember the frustration of trying to figure it out (and, a bit, the frustration of only ever using it once.) I’ve recently gone back to the program as part of teaching in the classroom and it is so much better the second time around. I suspect students would need help getting over the learning curve frustration – probably with an in class demonstration or self-paced document. They could figure it out on their own, but it would be a difficult thing to find the motivation to do so (without teacher guidance).
LikeLike
It is also very cool that the game introduced you to a new problem. I wonder how many things are in the game that are not always familiar to teachers and students that require extra research on the side. That is interesting and might get students more (or less) involved with the material.
LikeLike
That is one aspect of video games that is a fun side-note – the extent to which a video game creates interest in doing outside research. In some ways, I’ve been viewing video games as a way to creatively “practice” content covered in the classroom, but a game has the capacity to generate content and ideas to be investigated in the classroom.
LikeLike