You only get one first blog post…. right?
So don’t mss it up!
My name is Deron. I currently reside outside Twinsburg. I grew up in the suburbs of Detroit and moved to Cleveland with my wife (of now 22 years) in 2000 after law school. In addition to the two of us, we have two daughters and a dog that is far too spoiled for her own good.
I am coming to education as a second career. My first was practicing law and I eventually reached a point where I decided a change would be good… so I went and did the thing I always thought I’d do if I could do it over again – teach high school math. As a lawyer, I always thought the best part was talking with clients. My kids are nearly grown, which makes transitioning a bit easier. One is at OSU (which kinda kills me since I graduated from that school up north). The other is a high-school sophomore.
I learn best by doing and by puzzling the pieces together into a picture that makes orderly sense. I don’t do abstract learning particularly well (at least I don’t think so), so I’m always trying to find analogies that will help we relate abstract ideas to tangible ones.
I’m not sure I entirely know what is meant by taking intellectual risks. If it means risking time, energy and resources to investigate a new intellectual area that may not pay off, then I think I need only have confidence that someone who knows better than me will tell me when I am/have barked up the wrong tree for too long. If, on the other hand, it means taking the risk of offering a contrary viewpoint, then I only need the confidence that “good faith” is governing the conversation. With creative risk… allow me the time and tools and then be gentle in pointing out the design flaws.
I will admit that most of my reading has been in algebra and geometry textbooks lately, but I read a number of very thought provoking articles in Dr. Reynolds ED452 literacy class. One in particular- “Reading Mathematics: More than Words Can Say” by T. L. Adams – was a great reflection on the nature of mathematics as language, and how math has characteristics that are very common to other languages but is also subject to misunderstandings and misinterpretations. (The Reading Teacher, Vol. 56, No. 8 (May, 2003), pp. 786-795)
This, and other articles, have led me to think much more deeply about learning math as a literacy concept rather than just a content or logic matter. I am beginning to see where students are misinterpreting the language of math rather than failing in its processes or logic.
As for questions: Dr. Shutkin, what protocols do (or would) you follow in maintaining personal/professional social media profiles/blogs as an educator?




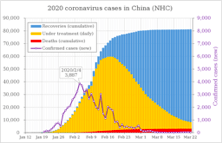







You must be logged in to post a comment.